ちょっとタイトルが意味不明な感じですが・・・
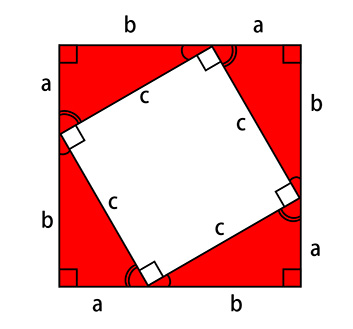
こんな感じで、正方形をθだけ回転したときの、回転した正方形を囲む正方形(c:c’)との辺の比を知りたい。ということで計算式を考えたのでメモ。
直角三角形では、ピタゴラスの定理が成り立つ(斜辺を c、他の辺を a,b としたとき、a*a+b*b=c*c)ので 元の三角形を囲む 4 つの直角三角形(赤い部分)は合同。また c’ = a + b となる。
【参考】ピタゴラスの定理 – Wikipedia
※「正方形を用いた証明」の項を参照。
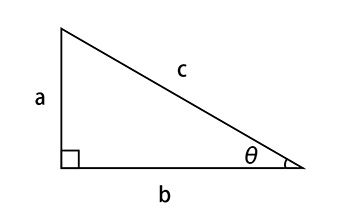
この赤い部分の直角三角形1つ取りだしてを考えると、 tanθ= a / b なので・・・ a = b * tanθ b = 1 / tanθ a*a+b*b=c*c なので、仮に c=1 とすると・・・ a = b * tanθ b = 1 / tanθ a*a+b*b=c*c なので、仮に a=1 とすると・・・ 1 *1 + (1 / tanθ)*(1 / tanθ) = c*c c = sqrt(1*1 + (1 / tanθ)*(1 / tanθ)) ここで外側の正方形の辺を 1 とし、それに対する内側の正方形の辺の比を n とすると、 c : a + b=n : 1 n = c / (a+b) = c / (1 + b) = 1*1 + (1 / tanθ)*(1 / tanθ) / (1 / tanθ) ※「sqrt」はルートを求めるための関数です。念のため。 ※ここで 仮に a=1 にしているのは、求めたいのは辺の長さではなくて、辺の比なので、たぶん問題ないはず。 とあるプログラムに組み込んで意図通り動いているので問題ないと思うけど、間違いがあればご指摘下さい。 【参考】直角三角形の1辺の長さと 角度はわかっています。90度 15度 75度、底辺の長さ... - Yahoo!知恵袋
【追記】2016.2.22
上の囲みの部分ですが、野中さんからご指摘を受けてもっとカンタンに考えられることがわかりましたので追記します。
この赤い部分の直角三角形1つ取りだしてを考えると、 sinθ= c / a cosθ= c / b tanθ= a / b なので、仮に c=1 とすると・・・ a = sinθ / 1 = sinθ b = cosθ / 1 = cosθ 1 = sinθ*sinθ + cosθ*cosθ ここで外側の正方形の辺を 1 とし、それに対する内側の正方形の辺の比を n とすると、 c : a + b = n : 1 1 : (sinθ+ cosθ) = n : 1 n = 1 / (sinθ+ cosθ)
※c = 1 とするのは、三角関数で一般的な単位円(半径 = 1)の考え方ですね。
【参考】sinとcosは何する関数? | Creators MeetUp vol. 22